混淆矩阵
目录
¶概述
大部分的机器学习指标(准确率、查准率、召回率、F1 值、ROC 曲线的 AUC 值)都可以直接或者间接的通过混淆矩阵进行计算。对于一个简单的二分类任务,可以得到下图的混淆矩阵(Confusion Matrix)
| Actual class | |||
|---|---|---|---|
| positive class | negative class | ||
| Predicted class | positive class | True Positive(TP) | False Positive(FP) |
| negative class | False Negative(FN) | True Negative(TN) | |
❓ 什么是混淆矩阵?
通过混淆矩阵,可以很直观地看清一个模型在各个类别(positive 和 negative)上分类的情况
| 真实类别为positive,模型预测的类别也为positive | |
|---|---|
| FP | 预测为positive,但真实类别为negative,真实类别和预测类别不一致 |
| FN | 预测为negative,但真实类别为positive,真实类别和预测类别不一致 |
| TN | 真实类别为negative,模型预测的类别也为negative |
¶准确率
准确率(Accuracy)计算公式如下:
$$
\text { accuracy }=\frac{T P+T N}{T P+T N+F P+F N}=\frac{T P+T N}{\text { all data }}
$$
¶精确率(查准率)和召回率(查全率)
positive class 的精确率 (precision) 计算公式如下:
$$
\text { precision }=\frac{T P}{T P+F P}=\frac{T P}{\text { 预测为 positive的样本 }}
$$
positive class 的召回率 (recall) 计算公式如下:
$$
\text { recall }=\frac{T P}{T P+F N}=\frac{T P}{\text { 真实为 positive的样本 }}
$$
positive class 的召回率只和真实为 positive 的样本相关,与真实为 negative 的样本无关;而精确率则受到两类样本的影响。
¶$F_1$ 值和 $F_{\beta}$ 值
$F_{1}$ 值的计算公式如下:
$$
F_{1}=\frac{2}{\frac{1}{\text { precision }}+\frac{1}{\text { recall }}}=\frac{2 \cdot \text { precision } \cdot \text { recall }}{\text { precision }+\text { recall }}
$$
$F_{1}$ 值就是精确率和召回率的调和平均值, $F_{1}$ 值认为精确率和召回率一样重要。
$F_{\beta}$ 值的计算公式如下:
$$
F_{\beta}=\frac{1+\beta^{2}}{\frac{1}{\text { precision }}+\frac{\beta^{2}}{\text { recall }}}=\frac{\left(1+\beta^{2}\right) \cdot \text { precision } \cdot \text { recall }}{\beta^{2} \cdot \text { precision }+\text { recall }}
$$
在 $\beta=1$ 时,$F_{\beta}$ 就是 $F_1$,此时 $F_\beta$ 认为 精确率和召回率一样重要,当 $\beta>1$ 时, $F_{\beta}$ 认为召回率更重要,当 $0<\beta<1$ 时,$F_{\beta}$ 认为精确率更重要
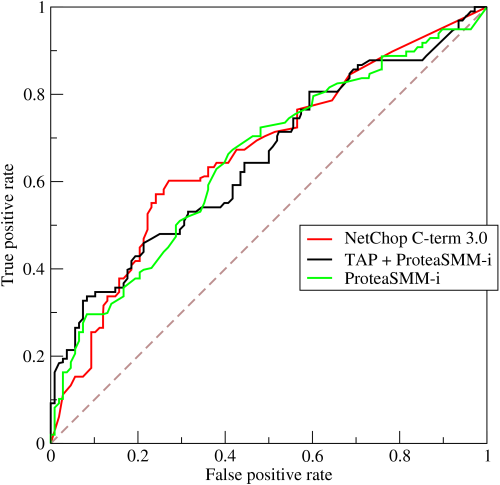
¶ROC 曲线及其 AUC 值
AUC 全称为 Area Under Curve,表示一条曲线下面的面积,ROC 曲线的 AUC 值可以用来对模型进行评价
ROC 曲线的纵坐标 True Positive Rate (TPR) 在数值上就等于 positive class 的 recall, 记作 recall positive, 横坐标 False
Positive Rate (FPR) 在数值上等于(1-negative class 的 recall), 记作 $(1$ - recall negative $)$ 如下所示:
$$
\begin{aligned}
\text { TPR } &=\frac{T P}{T P+F N} \
&=\text { recall }_{\text {positive }}
\end{aligned}
$$
$$
\begin{aligned}
\mathrm{FPR} &=\frac{F P}{F P+T N}=\frac{F P+T N-T N}{F P+T N} \
&=1-\frac{T N}{F P+T N} \
&=1-\text { recall }_{\text {negative }}
\end{aligned}
$$
通过对分类阈值 $\theta$ (默认 0.5)从大到小或者从小到大依次取值,我们可以得到很多组 TPR 和 FPR 的值,将其在图像中依次画出就可以得到一条 ROC 曲线,阈值 $\theta$ 取值范围为[0,1]。
ROC 曲线在图像上越接近左上角(0,1)模型越好,即 ROC 曲线下面与横轴围成的面积(AUC 值)越大越好。直观上理解,纵坐标 TPR 就是 $recall_{positive}$ 值,横坐标 FPR 就是$(1-recall_{negative})$,前者越大越好,后者整体越小越好,在图像上表示就是曲线越接近左上角(0,1)坐标越好。