目录

  1. 简介
  2. 并查集操作
    1. 添加
    2. 查询
    3. 路径压缩优化（扁平化处理）
    4. 合并
    5. 按秩合并优化
  3. 时空复杂度分析
    1. 时间复杂度
    2. 空间复杂度
  4. 参考引用

简介

并查集(Union-find data structure)是一种特殊的数据结构，用于快速处理一系列没有重复元素的集合(Disjoint sets)之间的合并以及查询问题

✨并查集支持如下操作:

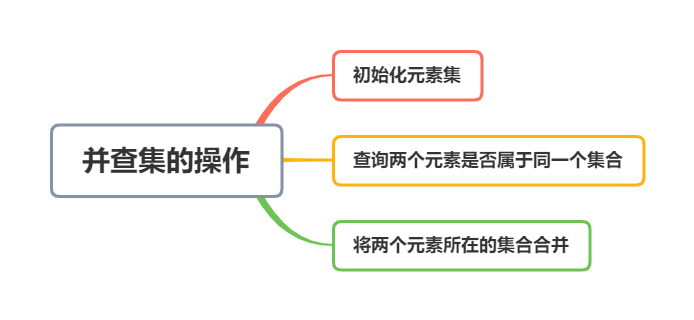
并查集的操作

并查集操作

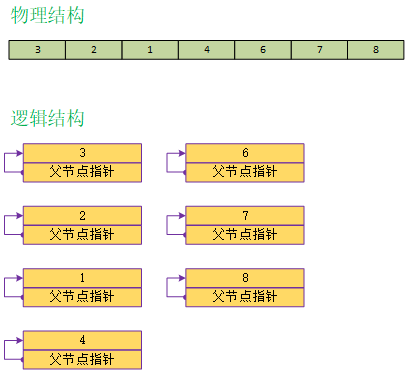
逻辑上，并查集将每一个集合以一棵树表示，每一个节点就是一个元素。节点保存着到它的父节点的引用，树的根节点则保存一个空引用或者到自身的引用或者其他无效值，以表示自身为根节点

添加

添加操作，makeSet(x)就是初始化操作，将x元素划分到属于仅有它自己的集合中，并且将父节点指向它自己。伪代码如下：

1
2
3
public  void makeSet(Element x){
    x.parent = x;
}

例如，通过初始化操作后，并查集逻辑结构如下：

🎶初始化并查集注意点:

  • 在经过优化的并查集中，添加操作还会初始化一些有关节点的信息，例如集合的大小
  • 并查集初始化的时候，要求用户把所有的数据都给程序

查询

在并查集中，每个集合存在一个代表元素，代表元素通常是集合的根节点。查询操作findHead(x)，从x开始，根据节点中父节点的引用，递归查找，伪代码如下：

1
2
3
4
5
6
7
public Element findHead(Element x){
    if(x.parent == x){
        return x;
    }else{
        return findHead(x.parent)
    }
}

🎶当集合很大或者树很不平衡时，上述代码效率很差，最坏的情况下（树退化成一条链），单次查询的时间复杂度高达(O(n) ,所以需要进行路径压缩。

路径压缩优化（扁平化处理）

路径压缩：在查询时(findHead)，将查询节点到根节点的路径上所有节点的父节点设置为根节点，从而减少树的高度。也就是说，在向上查询的同时，将路径上的每个节点都直接连接到根上，这样在以后查询时就可以直接查询到根节点。用伪代码表示如下：

1
2
3
4
5
6
7
8
public Element findHead(Element x){
    if(x.parent == x){
        return x;
    }else{
        x.parent = findHead(x.parent);
        return x.parent；
    }
}

合并

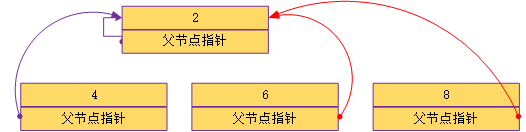
合并操作union(x,y)将元素x所在的集合与元素y所在的集合合并为一个。

首先，找出节点x与节点y对应的两个根节点，如果两个根节点其实是同一个，则说明元素x与元素y已经位于同一个集合中，否则，使其中一个根节点称为另一个的父节点,伪代码如下：

1
2
3
4
5
6
7
public void union(Element x,Element y){
    xRoot = findHead(x);
    yRoot = findHead(y);
    if(xRoot != yRoot){
        xRoot.parent = yRoot;
    }
}

🎶单纯的合并，可能使得树变得不平衡，增加树的深度，从而增加查询的耗时,需要对树的深度进行优化

按秩合并优化

控制树的深度的办法是：在合并时，比较两棵树的大小，较大的树的根节点成为合并后树的根节点，较小的一棵树的根节点则成为前者的子节点

✨树的大小有两种常用的衡量方式:

  • 以树中元素的数量作为树的大小（这被称为按大小合并）
  • 使用秩来比较树的大小

🎶基于秩的比较规则：

  • 只有根节点的树（即只有一个元素的集合），秩为 0
  • 当两个秩不同的树合并后，新的树的秩为原来两个树的秩的较大者
  • 当两个秩相同的树合并后，新树的秩为原树的秩加一

在合并时根据两棵树的秩的大小，决定新的根节点，这被称作按秩合并，用伪代码表示如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public  void makeSet(Element x){
    x.parent = x;
    x.rank = 0;
}
public void union(Element x,Element y){
	xRoot = findHead(x);
    yRoot = findHead(y);
    if(xRoot != yRoot){
        if(xRoot.rank<yRoot.rank){
            large = yRoot;
            small = xRoot;
        }else{
			large = xRoot;
            small = yRoot;
        }
        small.parent = large;
        if(large.rank == small.rank){
            large.rank = large.rank + 1;
        }
    }
}

🎶如果没有采用路径压缩优化，树的秩等于树的深度减一，使用路径压缩后，树的秩能反映出树的深度和大小。

时空复杂度分析

本小节主要介绍并查集结构的时空复杂度，并不会给予详细的证明，会用就行 😃

时间复杂度

经过优化的不交集森林（并查集）有线性的空间复杂度(O(n),n 为元素数目)，以及接近常数的单次操作平均时间复杂度 O($\alpha({n})$)

👴$\alpha({n})$称为反阿克曼函数,反阿克曼函数的特点就是，$n\to\infty$,$\alpha(n)<5$,所以可以大致认为，并查集的操作是 O(1)的时间复杂度

🎶同时使用路劲压缩和秩合优化的并查集，每次查询的合并操作的平均时间复杂度仅为 O($\alpha({n})$)

✨并查集编码特点：

  • findHead调用的越多，其他操作能够认为是 O(1)
  • findHead调用越频繁，复杂度逼近 O(N),但是其他操作的时间复杂度就越快

空间复杂度

并查集的空间复杂度是 O(n)，与初始化时输入数据的规模相关

参考引用

wiki