目录

1. 简介
2. 大根堆
3. 堆的操作
   1. 插入操作
   2. 删除操作
   3. 调整某个点的权值
4. 堆的实现
   1. heapInsert从下至上的调整
   2. heapify从上至下的调整
   3. 建堆
      1. 向上调整堆的方式建立堆
      2. 向下调整堆的方式建立堆
   4. 堆排序
5. 堆的进阶

本文的大部分内容抄录自OI Wiki

照例，先从一道经典例题开始：设计一个找到数据流中第 k 大元素的类（class）。注意是排序后的第 k 大元素，不是第 k 个不同的元素

¶简介

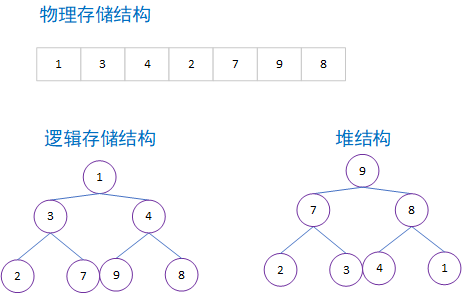
逻辑结构下，堆是一棵树，并且每个节点都保存有需要比较的值，这些节点间的关系不同，会产生不同的堆（如果没有特别声明，这里说明的堆都是常用的二叉堆）

❓什么是二叉堆？

📖既然已经存在树型结构了，为什么还需要堆结构尼？

¶大根堆

正如之前所说，如果每个节点的值都小于等于其父亲的键值，称之为大根堆，反之称为小根堆

🎶在堆上进行节点元素间的比较时，并非一定是数学上的大小比较，用户可以自定义大小比较关系

✨(大根)堆支持如下操作:

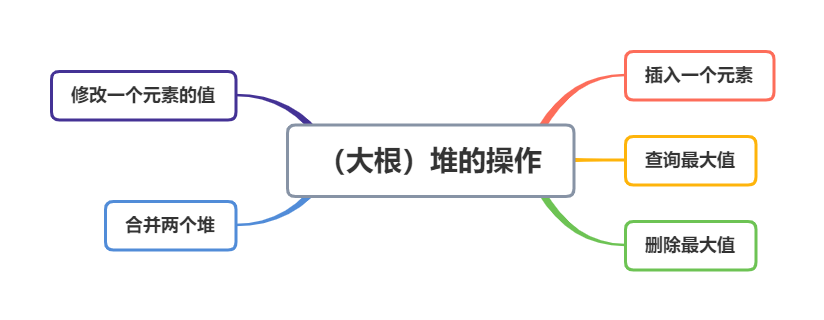
🎶以上均是堆支持的普通操作，可能存在专门用于解决某类问题而有意设计的堆；如合并堆支持高效地合并操作、有的堆还可以对任意历史版本进行查询或者操作。习惯上，堆往往指的都是二叉堆

¶堆的操作

本小节将详细介绍堆的常见操作

¶插入操作

⛵插入操作的步骤:

❓什么是向上调整?

具体的流程如下：

¶删除操作

堆的删除是考虑的插入操作的逆过程：将根结点与最后一个结点交换，然后直接删除。具体的细节如下：

❓什么是向下调整？

¶调整某个点的权值

¶堆的实现

堆的实现主要依赖于两个核心：向上调整和向下调整，可以使用数组（ $h$ ）来表示堆， $h_i$ 的两个儿子分别是 $h_{2i}$ 和 $h_{2i+1}$，那么图中下标 $1$ 是根节点

¶heapInsert从下至上的调整

1
2
3
4
5
6

private void heapInsert(int index) {
	while (index > 0 && heap[index] > heap[(index - 1) / 2]) {
		swap(index, (index - 1) / 2);
		index = (index - 1) / 2;
	}
}

¶heapify从上至下的调整

1
2
3
4
5
6
7
8
9
10
11
12
13
14

private void heapify(int index) {
	while (index * 2 + 1 < capacity) {
		int leftChildIndex = index * 2 + 1;
		if (leftChildIndex + 1 < capacity &&
               heap[leftChildIndex + 1] > heap[leftChildIndex]) {
			leftChildIndex += 1;
		}
		if (heap[leftChildIndex] <= heap[index]) {
			break;
		}
		swap(index, leftChildIndex);
		index = leftChildIndex;
	}
}

¶建堆

从一个空的堆开始，插入 $n$ 个元素，直接一个一个插入元素需要 $O(n \ long \ n)$ 的时间复杂度，存在两种不同的建堆方法

¶向上调整堆的方式建立堆

首先将元素全部拷贝完成后，从根结点开始，自下而上的调整

1

for (i = 0; i < capacity; i++) heapInsert(i);

对于第 $k$ 层的结点，向上调整的复杂度为 $O(k)$ 而不是 $O(log \ n)$ ，总的建堆时间复杂度为： $O(n \ log \ n)$

¶向下调整堆的方式建立堆

从叶子结点开始，逐个自下而上的调整堆

1

for (int i = capacity - 1; i >= 0; i--) heapify(i);

就样的操作就是将两个堆进行合并，能够做到 $O(n)$ 时间复杂度建堆

¶堆排序

1
2
3
4
5
6
7
8
9
10

public int poll() {
       //删除堆顶元素
	swap(0, capacity - 1);
	capacity = capacity - 1;
	heapify(0);
	return heap[capacity];
}
   for (int i = 0; i < 10; i++) {
	myHeap.poll();
}

📓有些场景就需要手写堆，才能做到高效解题的效果。例如，一个堆的问题，需要人为改写堆上的元素，这时就需要重新手写一个堆进行调整（比如图论中的 Dijkstra 算法可以使用堆进行加速）

¶堆的进阶