单调队列

目录

1. 概述
2. 基本思想
3. 基本操作
   1. push() 操作
   2. getMax()操作
   3. pop()操作
   4. 总结
4. 复杂度分析
5. 案例解答
6. 附录

特殊的数据结构就是用来处理特殊的问题，介绍单调队列之前，先来查看这样一种问题

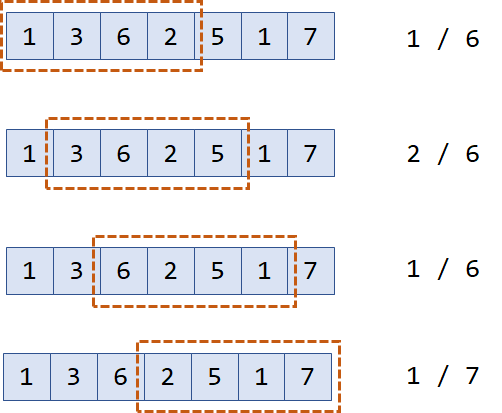
给你一个整数数组 nums，有一个大小为 k 的窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位，编程输出每 $k$ 个连续的数种的最大值和最小值

滑动窗口最大值Sliding Window

最朴实的想法就是：对于每一段长度为$i\sim i+k-1$ 的子数组，逐个比较来找出最大值和最小值，最终实践复杂度约为 $O(n \times k)$，这其中进行了大量的比较工作，那么是否存在一种比较边界的方法尼？答案是：存在，就是单调队列

¶概述

❓什么是单调队列？

单调队列仍然是一个队列，不过是对队列增强了一些限制（队列中的元素必须是单调增加或者单调降低的），与单调栈的关系类似。单调队列只是使用了一点巧妙的方法，使得队列中的元素单调递增（或递减）

✨单调队列主要用于解决滑动窗口类问题的数据结构，即：在长度为 $n$ 的序列中，求每个长度为 $m$ 的区间的区间最值，它的时间复杂度是 $O(n)$

¶基本思想

单调队列的基本思想是：维护一个双向队列（deque），遍历序列，仅当一个元素可能成为某个区间最值时才保留它

¶基本操作

一个单调队列提供的 API 原型如下，为了更好的演示，默认单调队列是单调递减的（队头元素是当前窗口的最大值）

public class MonotonicQueue {
	/** 双向队列 **/
	LinkedList<Integer> monotonicQueue;

	/** 初始化单调队列 **/
	public MonotonicQueue() {}

	/** 向单调队列种存入元素 **/
	public void push(int value) {}

	/**
	 * 获取单调队列种的最大值
	 **/
	public int getMax() {}

	/** 如果队头元素是 n 删除它 **/
	public void pop(int value) {}
}

💡对于这种取值，查值的操作，通常存储每个值的索引比存储值本身带来的效果更好，由于需要演示，所以这里采用的还是存储值的方式，而不是存索引的方式

¶push() 操作

向单调队列的尾部添加一个元素，如果添加的元素比队尾元素大，弹出队尾元素

/** 向单调队列种存入元素 **/
public void push(int value) {
   while (!monotonicQueue.isEmpty() && monotonicQueue.peekLast() < value) {
      monotonicQueue.removeLast();
   }
   monotonicQueue.offer(value);
}

¶getMax()操作

最终单调队列中的元素大小会保持一个单调递减的顺序，因此直接获取队列头结点就可以了（不考虑队列空的情况）

/**
* 获取单调队列种的最大值
**/
public int getMax() {
	return monotonicQueue.peekFirst();
}

¶pop()操作

删除操作是一种伪操作，由于某一个元素在入队的时候，可能造成其他元素的出队，所以这里的出队操作就是检查要出队的元素否为最大值（只有最大值的才会真正的出队，如果当前元素并不是最大元素，一定已经在最大元素入队的时候删除）

/** 如果队头元素是 value 删除它 **/
public void pop(int value) {
    if (!monotonicQueue.isEmpty() && monotonicQueue.peekFirst() == value) {
        monotonicQueue.removeFirst();
    }
}

¶总结

public class MonotonicQueue {
   /** 双向队列 **/
   LinkedList<Integer> monotonicQueue;

   /** 初始化单调队列 **/
   public MonotonicQueue() {
      monotonicQueue = new LinkedList<>();
   }

   /** 向单调队列种存入元素 **/
   public void push(int value) {
      while (!monotonicQueue.isEmpty() && monotonicQueue.peekLast() < value) {
         monotonicQueue.removeLast();
      }
      monotonicQueue.offer(value);
   }

   /**
    * 获取单调队列种的最大值
    *
    * @return 如果队列为空返回 -1,否则返回当前单调队列最大的元素
    **/
   public int getMax() {
      return monotonicQueue.peekFirst();
   }

   /** 如果队头元素是 value 删除它 **/
   public void pop(int value) {
      if (!monotonicQueue.isEmpty() && monotonicQueue.peekFirst() == value) {
         monotonicQueue.removeFirst();
      }
   }
}

¶复杂度分析

算法整体的复杂度依然是 $O(N)$ 线性时间，空间复杂度是 $O(K)$ 额外花费在窗口大小

¶案例解答

这里主要对上面的例题中求最大值进行coding，最小值一个思路，不过就是在插入元素时处理方式不同而已

public int[] maxSlidingWindow(int[] nums, int k) {
		int[] maxRecord = new int[nums.length - k + 1];
		LinkedList<Integer> monotonicQueue = new LinkedList<>();
		for (int i = 0; i < k; i++) {
            /**push()**/
			while (!monotonicQueue.isEmpty() && nums[monotonicQueue.peekLast()] < nums[i]) {
				monotonicQueue.removeLast();
			}
			monotonicQueue.offer(i);
		}
    	/**getMax()**/
		maxRecord[0] = nums[monotonicQueue.peekFirst()];
		for (int i = k; i < nums.length; i++) {
			while (!monotonicQueue.isEmpty() && nums[monotonicQueue.peekLast()] < nums[i]) {
				monotonicQueue.removeLast();
			}
			monotonicQueue.offer(i);
			while (monotonicQueue.peekFirst() <= (i - k)) {
				monotonicQueue.removeFirst();
			}
			maxRecord[i - k + 1] = nums[monotonicQueue.peekFirst()];
		}
		return maxRecord;
}

其实以上代码就是LeetCode.239. 滑动窗口最大值

¶附录

算法学习笔记(66): 单调队列

特殊数据结构：单调队列

单调队列