目录

  1. 位运算的加
  2. 位运算的减
  3. 位运算的乘
  4. 位运算的除
  5. Brian Kernighan 算法
  6. 格雷码（Gray Code）
  7. 将一个数的最低位变成 0
  8. 消去一个数的最后一位 1
  9. 附录

主要记录位运算下的常用算法

位运算的加

位运算的减

位运算的乘

位运算的除

Brian Kernighan 算法

Brian Kernighan 算法用于计算某数（ $x$ ）比特数中含有的 $1$ 的个数

Brian Kernighan 算法的原理是：对于任意整数 $x$，令 $x=x\&(x-1)$ ，该运算将 $x$ 的二进制表示的最后一个 1 变成 0。因此，对 $x$ 重复该操作，直到 $x$ 变成 0，则操作次数即为 $x$ 的一比特数

1
2
3
4
5
6
7
8
public int brianKernighan(int n){
    int res = 0;
    while(n>0){
        res++;
        n = n&(n-1);
    }
    return res;
}

格雷码（Gray Code）

n 位格雷码序列 是一个由 $2^n$ 个整数组成的序列，其中：

  • 每个整数都在范围 $[0, 2^{n}-1]$ 内（含 $0$ 和 $2^{n}-1$ ）
  • 第一个整数是 0
  • 一个整数在序列中出现 不超过一次
  • 每对相邻整数的二进制表示恰好一位不同 ，且第一个和最后一个整数的二进制表示恰好一位不同
LeetCode 89.格雷编码

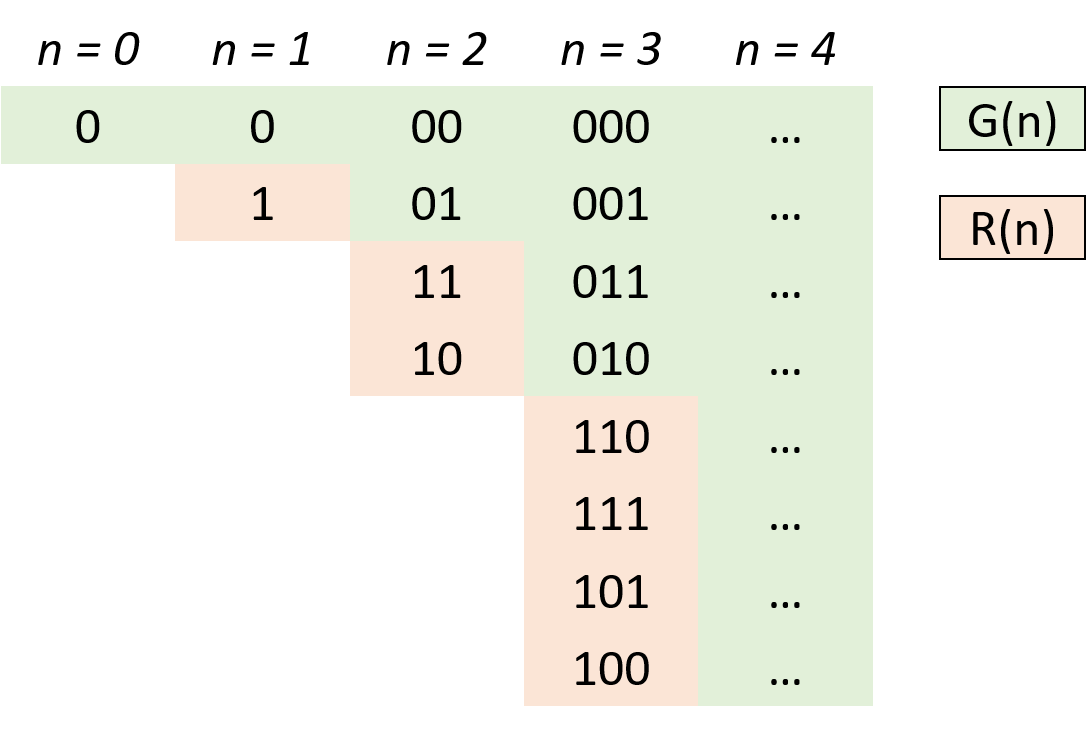
使用镜像反射法能够生成格雷码[1],具体的思想是不断的从 n 位格雷码，生成 n+1 位格雷码，其中 n+1 位格雷码的前一半是 n 位格雷码，后一半是前一半格雷码的二进制最高位为 1 的数字，如下：

将一个数的最低位变成 0

n & (n - 1),其预算结果恰为把 $n$ 的二进制位中的最低位的 1 变为 0 之后的结果

消去一个数的最后一位 1

n & ((~n) +1) 能够取得 n 到最右边的 1

附录

  1. https://leetcode-cn.com/problems/gray-code/solution/gray-code-jing-xiang-fan-she-fa-by-jyd/ ↩︎