目录 概述 时间复杂度${O(n^2)}$ 时间复杂度${O(n)}$ 循环左移 完美洗牌扩展 附录 概述 有个长度为 2n 的数组 ${a1,a2,a3,…,an,b1,b2,b3,…,bn}$,希望排序后 ${a1,b1,a2,b2,….,an,bn}$ ,请考虑有无时间复杂度$O(n)$,空间复杂度$O(1)$的解法
时间复杂度${O(n^2)}$ ⛵ 通过双重循环,逐个确定${b1,b2,b3,b4}$的位置,具体步骤如下:
确定${b1}$的位置,即让${b1}$跟它前面的${a2,a3,a4}$交换 -> ${a1,b1,a2,a3,a4,b2,b3,b4}$ 确定 ${b2}$ 的位置,即让 ${b2}$跟它前面的 ${a3,a4}$ 交换 -> ${a1,b1,a2,b2,a3,a4,b3,b4}$ 确定 ${b3}$ 的位置,即让 ${b3}$ 跟它前面的 ${a4}$ 交换 -> ${a1,b1,a2,b2,b3,a3,a4,b4}$ ${b4}已在最后的位置,不需要再交换。如此,经过上述 3 个步骤后,得到最后想要的序列 时间复杂度${O(n)}$ 2004 年,microsoft 的 Peiyush Jain 在他发表一篇名为:“A Simple In-Place Algorithm for In-Shuffle” 的论文中提出了完美洗牌算法。完美洗牌问题就是上述提出的需要解决的问题,不过最终排序后的元素不太一致而已,其实只要在完美洗牌问题的基础上对它最后的序列swap两两相邻元素即可。
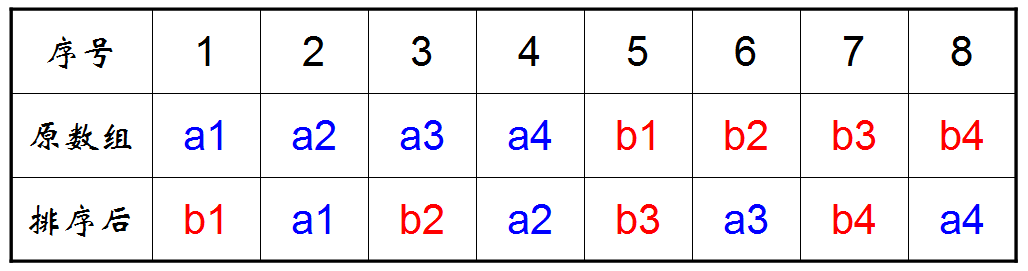
其实可以考虑,通过洗牌(shuffle)操作之后,每个位置上元素的变化如下:
1 2 3 4 5 6 7 8 a1:1 -> 2 a2:2 -> 4 a3:3 -> 6 a4:4 -> 8 b1:5 -> 1 b2:6 -> 3 b3:7 -> 5 b4:8 -> 7
对于原数组位置 i 的元素,新位置是 (2*i)%(2n+1)2n 表示原数组的长度,有了该表达式,困难不再是寻找元素在新数组中的位置,而是为该元素「 腾出位置 」。由于每一个位置都进行了变化,如果使用一个等长的数组拷贝的话,空间复杂度必然达不到要求,因此需要换个思路
类似于滚动数组的想法,a1 从位置 1 移动到位置 2,那么,位置 2 上的元素 a2 根据变化接着向下移动,继续这中滚动节奏,最终必然会得到一个「 封闭环 」
1 1 -> 2 -> 4 -> 8 -> 7 -> 5 -> 1
通过这个封闭环,可以将一些元素原地替换掉,随后继续进行下一个封闭环的就地替换,就能够完成就地的完美洗牌算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 void CycleLeader (int *a,int start, int n) { int pre = a[start]; int mod = 2 * n + 1 ; int next = start * 2 % mod; while (next != start){ swap(pre,a[next]); next = 2 * next % mod; } a[start] = pre; }
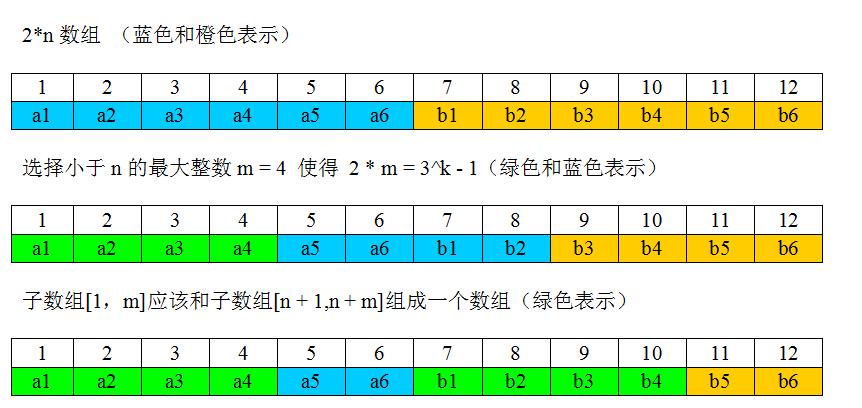
论文中给出了严谨的结论,对于 ${2*n = 3^k-1}$这种长度的数组,恰好有 $k$ 个环,且每个环的起始位置分别是 1,3,9,…,$3^{k-1}$
对于特定长度数组的完美洗牌算法完成了,那么如果数组的长度不满足上式条件如何进行?
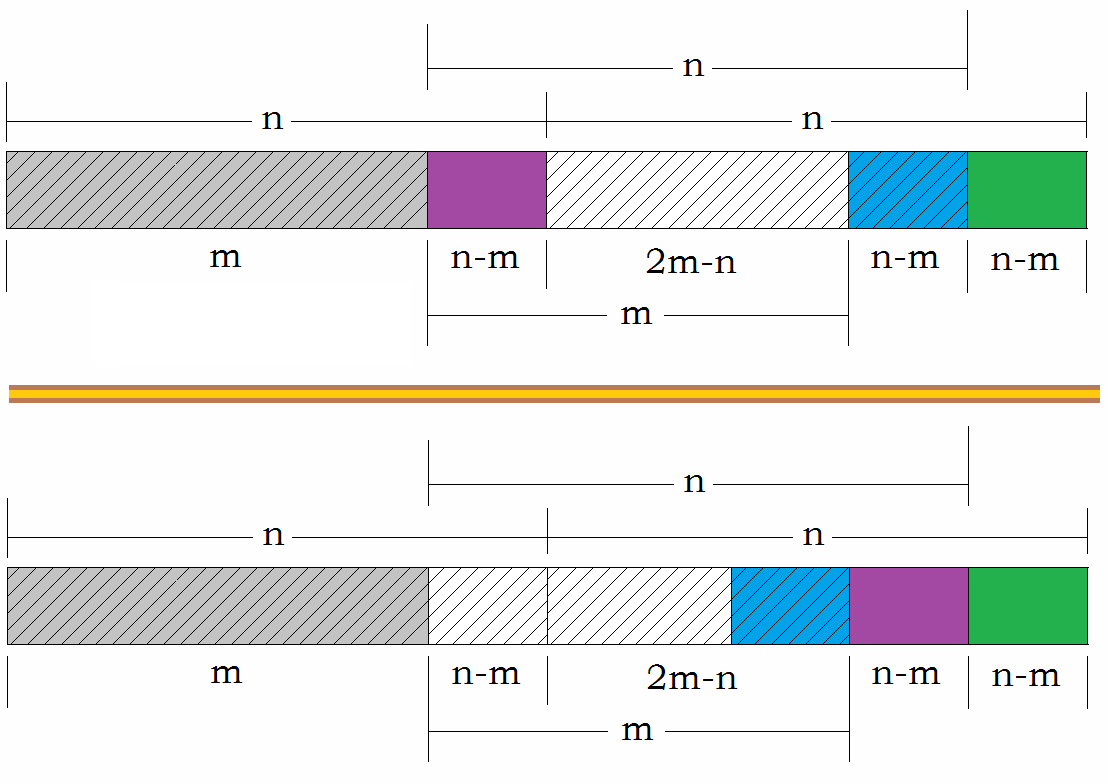
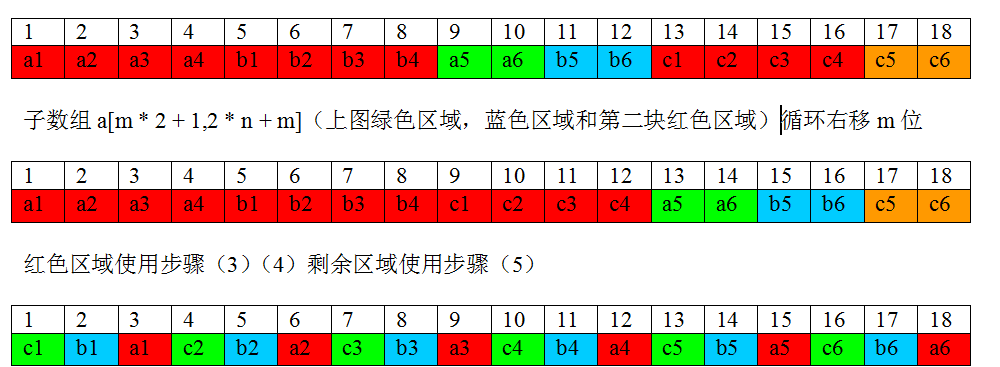
若 ${2n !=3^k-1}$,则总可以找到最大的整数 $m$,使得${ m < n }$,并且 ${ 2m = 3^k-1}$,其中对于长度为 2m 的数组,调用封闭环内就地完美洗牌算法即可,剩余的2(n-m)长度,递归调用子数组的完美洗牌步骤即可,具体的例子如下:
下面使用[a,b]表示从 a 到 b 到一段子数组,包括端点,
图中斜线阴影部分的子数组[1,m]应该和[n + 1,n + m]组成一个数组,调用封闭环上的走圈算法 数组[m+1,m+n]循环左移 n-m次即可(数组的循环位移是存在空间复杂度为 O(1),时间复杂度为 O(n)的算法) 原始问题要输出$a1,b1,a2,b2……an,bn$,而完美洗牌却输出的是$b1,a1,b2,a2,……bn,an$。解决办法非常简单:忽略原数组中的$a1$和$bn$,对于$a2,a3,……an,b1,b2,……bn-1$调用完美洗牌算法,即为结论
举个例子,n=6,${a1,a2,a3,a4,a5,a6,b1,b2,b3,b4,b5,b6}$
其中步骤(3)(4)就是封闭环中的走圈算法,步骤(5)就是子数组的递归划分算法
循环左移 上面步骤中,用到了时间复杂度$O(n)$,空间复杂度$O(1)$的循环移位操作,具体的思路如下:
假设循环左移 m 位,将数组分成两段,第一段位前 m 个元素,第二段为剩余的元素。将第一段和第二段各自翻转一下,再将整体翻转一下即可做到循环左移的操作
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 void Reverse (int *a,int start,int end) { while (start < end){ swap(a[start],a[end]); ++start; --end; } } void LeftRotate (int *a,int m,int n) { Reverse(a,1 ,m); Reverse(a,m+1 ,n); Reverse(a,1 ,n); }
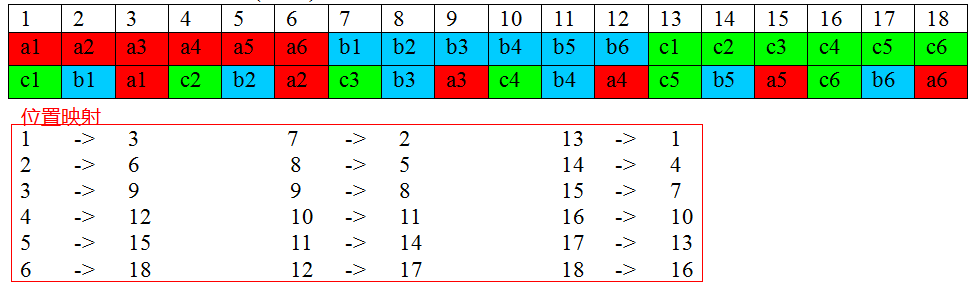
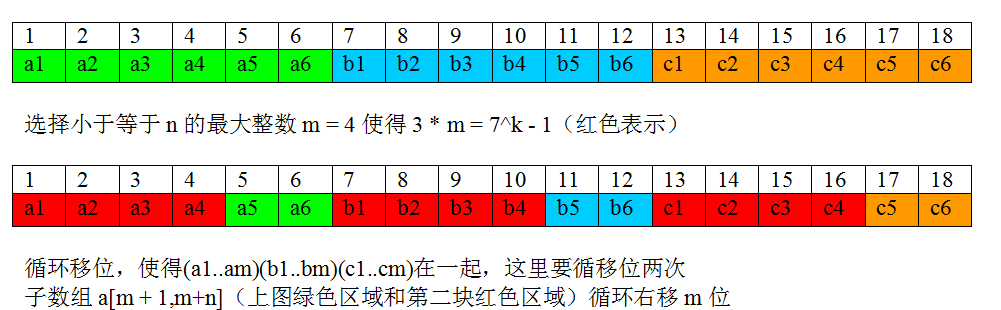
完美洗牌扩展 如果输入是$a1,a2,……an, b1,b2,……bn, c1,c2,……cn$,要求输出是$c1,b1,a1,c2,b2,a2,……cn,bn,an$怎么办?
其实这个问题的本质与之前描述的完美洗牌算法没有什么不同,同样分析其规律就可以了
对于原数组位置 i 的元素,新位置是(3*i)%(3n+1)
附录 完美洗牌算法